Day 1: Historian Hysteria

This post walks through solving Advent of Code 2024 - Day 1 Problem in Clojure.

Another year, another exciting challenge — Advent of Code 2024 is here! As always, it’s time to flex those problem-solving muscles and dive into a festive season of coding fun.

As always, Advent of Code greets us with a whimsical storyline—this time involving yet another absurdly complicated holiday crisis. Who knew saving Christmas could be so dependent on our coding skills every single year!

Part One

We’re tasked with comparing two lists of numbers. The goal is to pair the smallest number from the left list with the smallest from the right, the second-smallest with the second-smallest, and so on.

For each pair, we calculate the absolute difference between the numbers and sum all those distances to get the final result.

To dive deeper into the details of the Day 1 challenge, check out the official problem description.

Day 1 kicks off with a classic warm-up puzzle, setting the stage for the challenges ahead. Let’s break it down, analyze the problem, and craft an elegant solution to get our Advent of Code journey started!

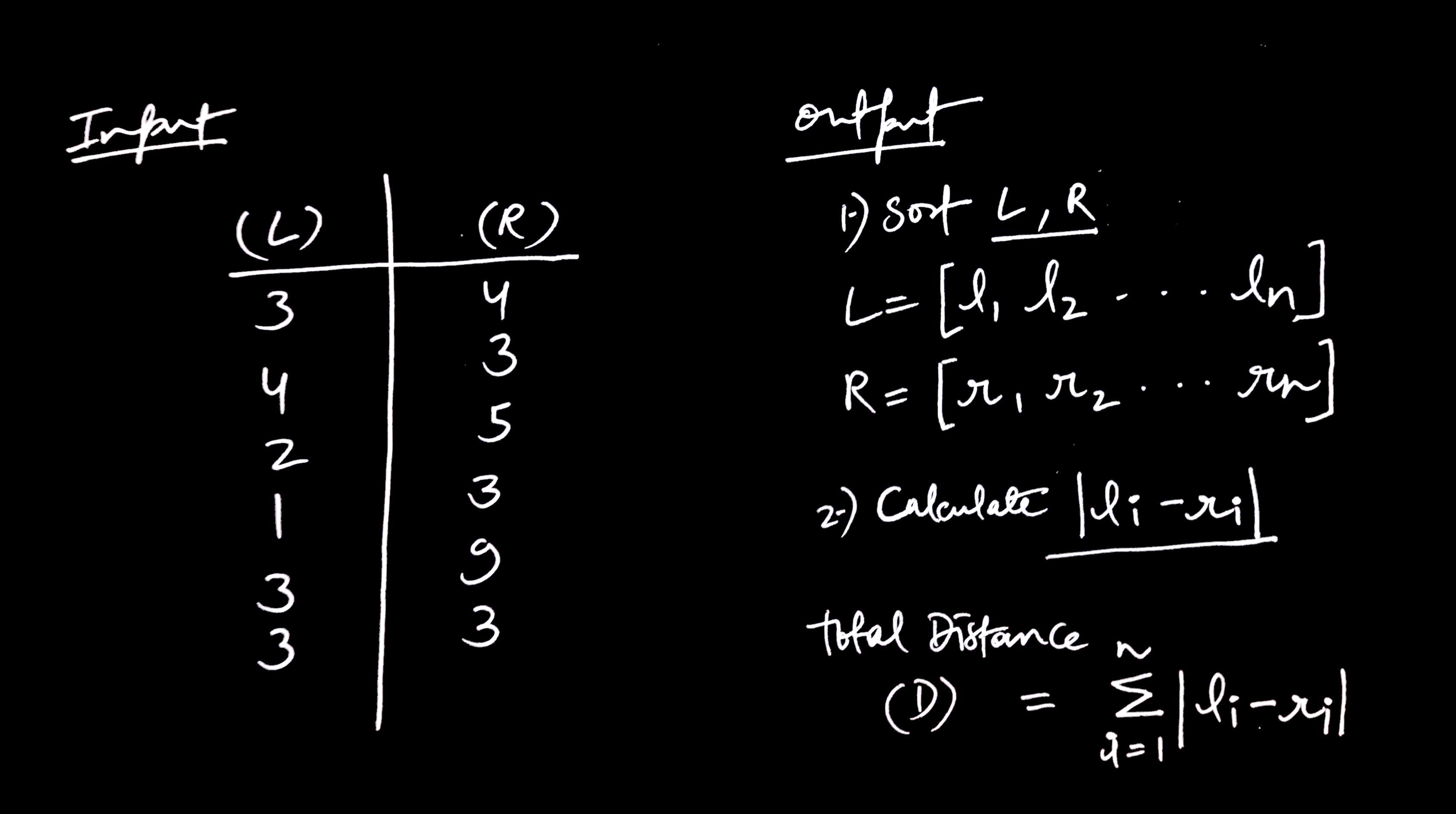
**Fig 1.1: Input/Output Representation of Problem**

Below Clojure code reads the input from a file, splits it into lines, and then processes each line by splitting it into individual numbers and converting them to integers.

(ns aoc.2024.d1.d1
  (:require [clojure.string :as s]))

(def data (->> "input.txt"
               slurp
               s/split-lines
               (map #(map read-string (s/split % #"\s+")))

Below code transposes the list of lists and sorts the elements of each resulting group, preparing the data for the next step in the problem.

               (apply map vector)
               (map sort)))

This part of the code is performing two main operations on the data:

(apply map vector): This takes the list of lists and transposes it. Essentially, it transforms the rows of a matrix into columns. If you had a list of pairs like [[a b] [c d] [e f]], after applying map vector, it would become [[a c e] [b d f]]. It groups elements at the same index from each sublist into a new list.
(map sort): After transposing the lists, it sorts each inner list in ascending order. So, each individual sublist is sorted, ensuring the numbers within each pair or group are in the correct order.

Then, below code calculates the sum of the absolute differences between corresponding elements from two lists, first data and second data, by mapping each pair of elements through subtraction and taking the absolute value, reducing the result with a summation.

(reduce + (map #(abs (- %1 %2)) (first data) (second data)))

Let’s break it down:

(first data) and (second data): This extracts the first and second elements of the data structure (likely a vector of lists). If data is a vector like [[1 2 3] [4 5 6]], first data will give you [1 2 3] and second data will give you [4 5 6].
(map #(abs (- %1 %2)) (first data) (second data)): This creates a new sequence where each pair of values from the two lists is subtracted, and the absolute value of the difference is taken. Map takes each pair of values (%1 from first data and %2 from second data), subtracts %2 from %1, and applies abs to the result.
reduce +: This will sum up all the values produced by the map. reduce applies the + function cumulatively to the list generated by the map.

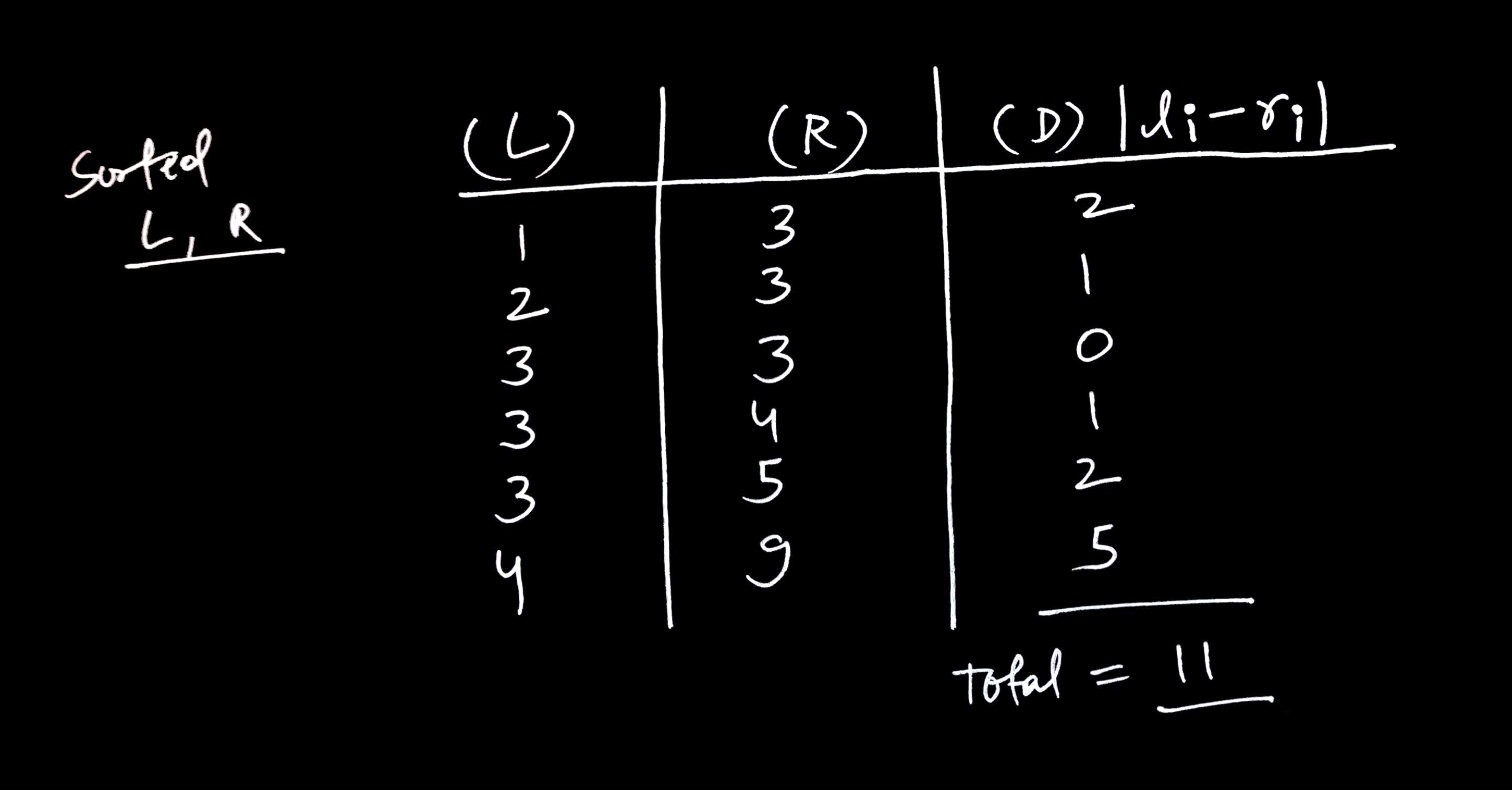
**Fig 1.2: Solution Representation of Problem**

And just when you think you’re done, part two swoops in like a plot twist, reminding you that Advent of Code is never that simple!

Part Two

The task is to calculate a similarity score by counting how often each number from the left list appears in the right list, then multiplying each number in the left list by its frequency in the right list, and finally summing these products.

**Fig 1.3: Similarity Score Representation**

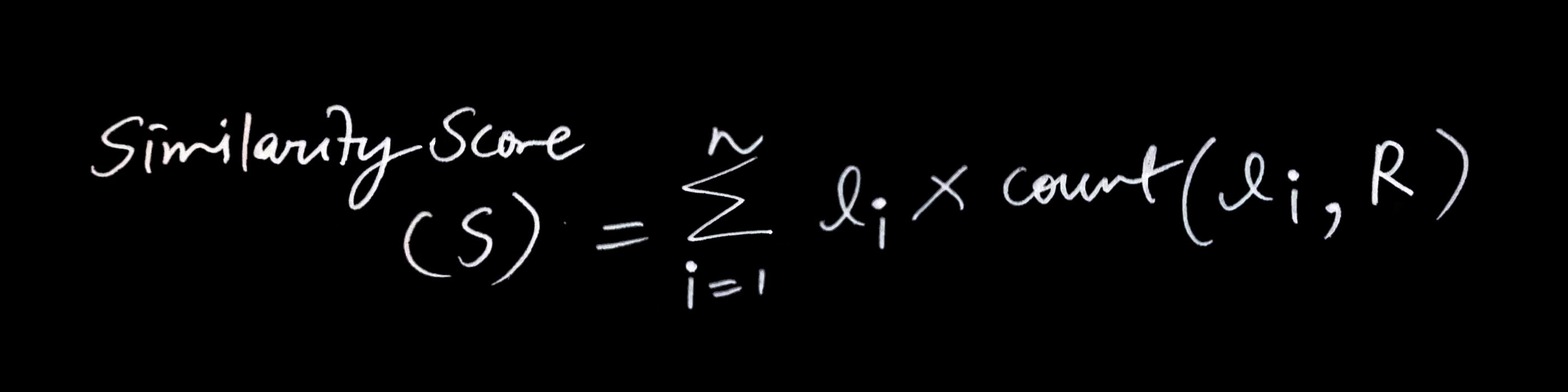
To calculate the similarity score, we first need to determine how often each number from the right list appears. This is where the frequencies function comes in handy.

(def f (frequencies (second data)))

frequencies: This function generates a map where each key is an element from the right list (second data), and the associated value is the count of occurrences of that element in the list.

So, f will store a map of the frequencies of each number in the right list. For example, if the second list is [1 2 2 3], f will be {1 1, 2 2, 3 1}.

This frequency map is then used in the similarity score calculation, where each number in the left list is multiplied by its frequency in this map to compute the total similarity score.

(reduce + (map #(* (f % 0) %) (first data)))

Above code calculates the total similarity score by multiplying each element in the left list (the first list in data) by the frequency of that element in the right list (stored in the frequency map f).

Here’s a breakdown:

(f % 0): This fetches the frequency of the element % from the frequency map f. If the element doesn’t exist in the map, it defaults to 0, ensuring no error occurs if the element isn’t found.
(* (f % 0) %): This multiplies the element % from the left list by its frequency from the right list, giving the weighted contribution of each element to the similarity score.
(map #(* (f % 0) %) (first data)): This maps over the first list (first data), applying the multiplication for each element.
reduce +: Finally, reduce adds up all these weighted contributions to calculate the total similarity score.

Here’s the full source code for the solution, which combines all the steps we’ve discussed:

(ns aoc.2024.d1.d1
  (:require [clojure.string :as s]))

(def data (->> "input.txt"
               slurp
               s/split-lines
               (map #(map read-string (s/split % #"\s+")))
               (apply map vector)
               (map sort)))

;; Part 1
(reduce + (map #(abs (- %1 %2)) (first data) (second data)))

(def f (frequencies (second data)))

;; Part 2
(reduce + (map #(* (f % 0) %) (first data)))

And just like the story of Day 1 in Advent of Code — where two lists are mysteriously off by just a bit — we’ve navigated through the twists and turns of comparing elements, calculating differences, and weighing frequencies. A little Clojure magic later, and we’ve got a similarity score. But don’t get too comfortable — this is just the start, and Day 2 is ready to throw us another curveball!